- Introduction
- Introduction
- Explanation of two-point perspective: what it is, its meaning, definition, and a clear, easy-to-understand guide
- Calculation formula for the cone of vision
- The basic form of perspective drawing mainly used this time
- The difference between a rectangular prism and a cube: meaning, definition, and an easy-to-understand explanation
- The problem of not understanding the ‘reference point for determining the depth of a cube’
- Types of Methods for Drawing a Cube Using Two-Point Perspective
- Drawing a Cube Using the Measuring Point Method
- The question of where the point that determines the depth is located
- Find it using the ‘Measuring Point Line’
- Learn about the circumference, radius, diameter, center, etc., and understand the ‘slide’
- How to actually slide it
- Using the ‘Depth Reference Point (DRP)’ to determine the depth
- (1) draw an appropriate vertical line.
- (2) Extend the vertices to VP1 and VP2, that is, to the original vanishing points.
- (3) Draw lines of the same length as the vertical line to the left and right
- (4) Extend A toward MP2 and B toward MP1 so that they intersect
- (5) All that remains is to complete the cube.
- The completed cube
- Drawing a Cube Using the Medium Line Method
- Do the Measuring Point Method and Medium Line Method Align?
- Drawing a Cube Using the Ground Line Method
- What is a baseline? Meaning, definition, and an easy-to-understand explanation
- Where is the baseline located within the picture plane?
- Drawing using the baseline method without a plan view
- (1) Draw the vertical line of the cube you want to draw.
- (2) Draw lines to each VP
- (3) Draw the ground line
- (4) Draw horizontal lines to the left and right with the same length as the vertical line you drew, forming a circle
- (5) Draw lines from the starting point to each VP, parallel to the line extending from SP to VP
- (6) Create a square based on the lines extended horizontally
- (7) Extend the sides of the square
- (8) Extend a line from the newly determined point to VP
- (9) Complete the cube
- The completed cube
- Do the “Measuring Point Method” and “Medium Line Method” Align with the Ground Line Method?
- Trying Other Cone of Vision and Angles
- Plans for the Next Session
- References
- Books that are easy for beginners to understand
- David Chelsea「Extreme Perspective! For Artists: Learn the Secrets of Curvilinear, Cylindrical, Fisheye, Isometric, and Other Amazing Drawing Systems that Will Make Your Drawings Pop Off the Page 」
- Robbie Lee「Perspective Made Easy: A Step-by-Step Guide」
- Scott Robertson「How to Draw: drawing and sketching objects and environments from your imagination」
- About the Japanese version of this article
- Books that are easy for beginners to understand
Introduction
Explanation in the video
The ‘Overview, Summary, or Conclusion’ of this article can be found at the beginning of the YouTube video, so please refer to it.
If possible, we would appreciate it if you could subscribe to our channel to help maintain the site. It serves as motivation for us!
Introduction
Let’s briefly review the previous lesson.
Explanation of two-point perspective: what it is, its meaning, definition, and a clear, easy-to-understand guide
POINTTwo-Point Perspective:A linear perspective method that uses two vanishing points, one on the left and one on the right.
In two-point perspective, vertical lines do not converge, while lines in the depth and horizontal directions converge toward two separate vanishing points.
This diagram organizes the types of two-point perspectives.
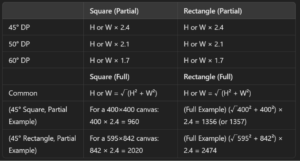
Calculation formula for the cone of vision
Let’s apply all the knowledge from the previous videos to create a two-point perspective drawing.
We’ll start with the basic ‘symmetrical two-point parallel perspective’ case. For simplicity, we’ll assume a canvas of 400×400 pixels as the basis for our drawing.
[Fourth Session] What is the cone of vision (COV) in perspective?
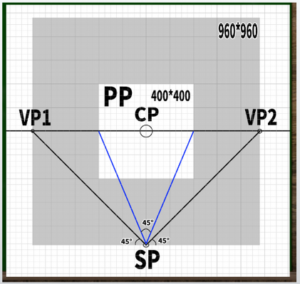
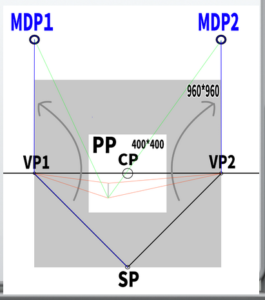
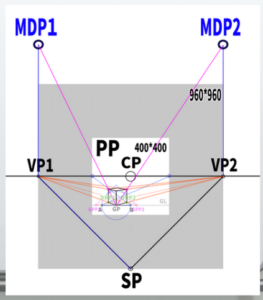
If we want to fit a 45-degree Cone of Vision perfectly onto a 400×400 screen (PP), we learned in the fourth video that the vanishing points approximately lie on the circumference of a 960×960 circle.
The calculation is 400 × 2.4 = 960.
※ To cover the entire screen with the Cone of Vision, use the formula X (side of the square) = √(width² + height²).
In this case, it equals 565, and multiplying it by 2.4 results in 1356.
For this example, we’ll use 960.
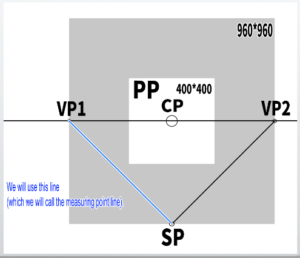
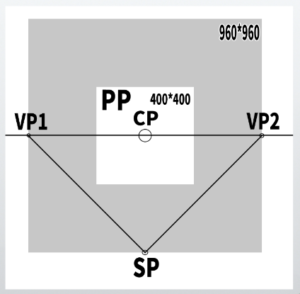
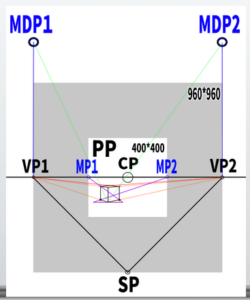
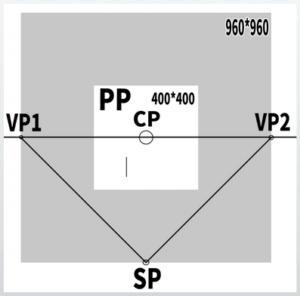
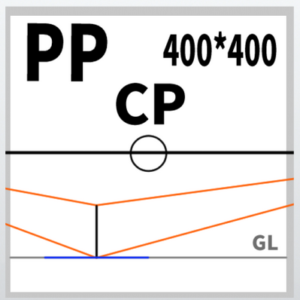
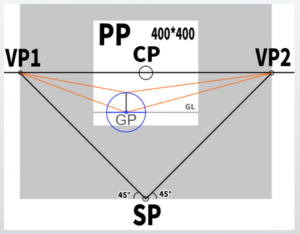
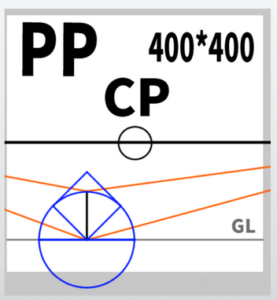
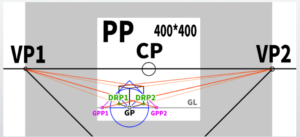
The basic form of perspective drawing mainly used this time
This is how it looks in the diagram.
CP is the center of point, SP is the station point, VP are the vanishing points, and PP is the picture plane.
The difference between a rectangular prism and a cube: meaning, definition, and an easy-to-understand explanation
POINTCube (Regular Cube):A regular hexahedron where all six faces are squares. The lengths of all edges are equal, and all angles are right angles (90°).
POINTRectangular Prism:A three-dimensional shape composed of six rectangular faces. Two opposite faces are congruent and parallel, and all angles are right angles (90°).
A cube is a special case of a rectangular prism. There are various types of rectangular boxes, but the one where all edges are equal, like a die, is specifically called a cube.
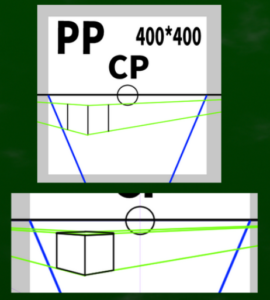
Now, drawing a ‘random rectangular prism’ is easy.
First, draw the vertical lines of the rectangular prism you want to create. Then, extend lines from those vertical lines towards the VP (vanishing point).
Next, just determine an ‘appropriate depth’ and create the rectangular prism.
At this point, we are not trying to draw a ‘regular cube.’ In other words, we are not aiming to draw a cube like a die where all the edges have equal measurements.
We have simply decided on the depth intuitively.
Of course, if we were to draw a rectangular prism with the correct proportions, that would be a different story, but right now we are just drawing it freely and intuitively.
However, it might be important to keep in mind that the skill of ‘making something look correct’ with freehand drawing is what truly matters.
In any case, if you don’t know the correct form, you won’t be able to develop the skill of noticing and correcting awkwardness through freehand.
Therefore, the process of drawing the correct form at least once should be beneficial.
For example, even if you don’t directly use the image in life drawing, the correct, natural, or beautiful proportions (relationships) beyond the specific object (element) will still be internalized, much like how accurate proportions are learned.
The problem of not understanding the ‘reference point for determining the depth of a cube’
If we are to draw a regular cube, we will need a ‘reference’ for where to set the depth.
However, the knowledge we’ve learned from the videos so far doesn’t provide that reference. Therefore, it is necessary to learn about the reference.
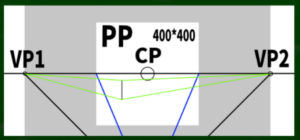
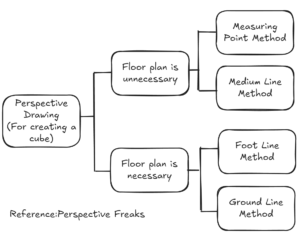
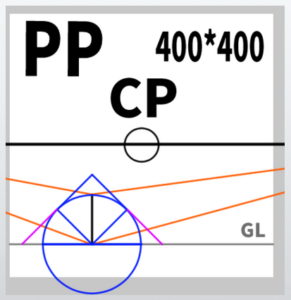
Types of Methods for Drawing a Cube Using Two-Point Perspective
Explanation with a diagram
In a diagram, this would look like the following.
By the way, the method used to create a cube in the previous video using one-point perspective is ‘measuring point method’ in this context, and it is specifically referred to as ‘distance point method (D-point method)’.
Since we haven’t yet dealt with the methods for floor plans in detail, this time we will focus on the measuring point method and medium line method, which don’t require a floor plan. The ground line method will be briefly addressed at the end.
It seems that the cube constructed using any of these methods will be the same.
In architecture, a floor plan would likely be prepared, but it is probably rare for people to draw a floor plan when drawing a picture (though this may be different for concept art, etc.).
Some people even avoid using floor plans when creating 3D models (especially for complex subjects like humans and nature, where an intuitive approach may work better).
What is the Measuring Point Method (M-point method)? Meaning, definition, and an easy-to-understand explanation
POINTMeasuring Point Method (M-Point Method):A perspective drawing method that uses measuring points.
POINTMeasuring Point (MP):A point that serves as an additional, convenient vanishing point. Positioned on a specific vanishing line (mainly the horizon line), it is used to accurately measure the dimensions of objects in perspective drawings.
Using this point allows for the measurement of actual lengths, taking perspective projection into account, regardless of the orientation or position of the object.
What is the Medium Line Method? Meaning, definition, and an easy-to-understand explanation
POINTMedium Line Method:A perspective drawing method that uses medium lines.
POINTMedium Line: A straight line that converges at a vanishing point with a 45-degree inclination angle. It can be considered a type of measuring point (convenient point). We will refer to this point as the ‘medium line point.’ To distinguish it from the measuring point, it will be abbreviated as MDP.
What about the difficulty of terms and explanations in perspective?
Now, having heard the definitions of the measuring point method and the medium line method, I still don’t understand at all.
Even when I look at the explanatory diagrams, I remain just as confused. Especially when geometric or mathematical elements come into play, I struggle as a humanities major.
It’s true that it’s possible to create a cube, but understanding ‘why it’s possible’ is difficult (I would like to address this in another video). It’s like how it’s possible to ride a train, but I don’t know why the train moves, and perhaps I don’t need to know either.
‘First, being able to create a cube using two-point perspective’ will be the turning point in deciding whether to give up learning perspective. For now, all I can do is keep experimenting. The act of ‘just drawing it’ is likely the key.
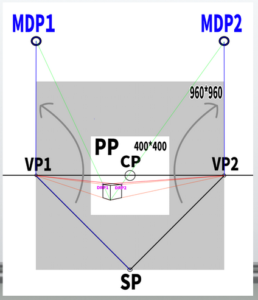
Drawing a Cube Using the Measuring Point Method
The question of where the point that determines the depth is located
To draw a cube, a ‘depth reference point’ is necessary. I understand that this reference point is the ‘measuring point (MP).’
Now, the question arises: ‘How do we determine the position of this measuring point?’
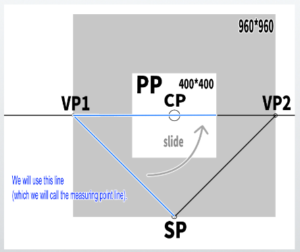
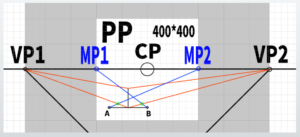
Find it using the ‘Measuring Point Line’
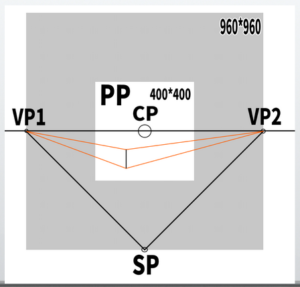
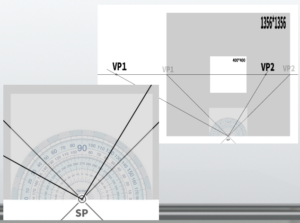
In the Measuring Point method, it seems that the line extending from SP to VP can be used.
Let’s call this line the ‘measuring point line.’ By sliding the measuring point line onto the horizon line, that becomes the measuring point.
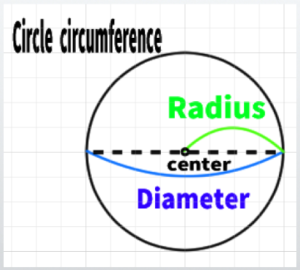
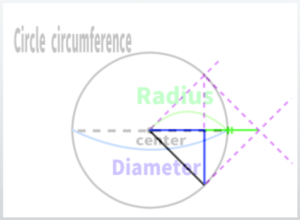
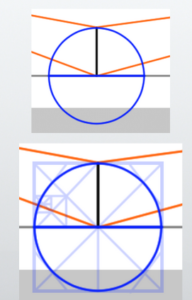
Learn about the circumference, radius, diameter, center, etc., and understand the ‘slide’
However, I have a question in my mind: What exactly does ‘sliding’ mean? The explanation that I can barely understand is, ‘Assume that VP1 is the center of a circle, and SP is one of the points on the circumference of that circle.’
But I’m unsure if the term ‘circumference’ is appropriate here. I will need to review this again.
Key terms related to circles are ‘radius,’ ‘diameter,’ and ‘circumference.’ I learned in elementary school that the area of a circle is found by multiplying the radius by itself and then by 3.14 (pi).
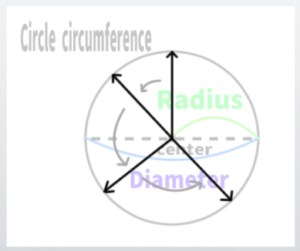
The line extending from the center of the circle to the circumference can be thought of in various ways. In the diagram from earlier, it would look like this.
You can imagine the line sliding as if the hands of a clock were moving. The key point is that each of these lines is of the ‘same length’ (in actual measurement).
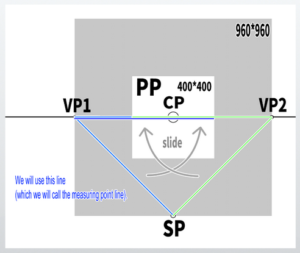
If we consider VP1 as the center of the circle and slide the line extending to SP along the horizon line (HL), it would look like this.
※We will not touch on the reasoning as to why the MP perfectly aligns with the edges of the 400×400 canvas in this case.
How to actually slide it
Although the concept of sliding is understood, the question of ‘how exactly to slide it’ will likely arise.
※Let’s put aside the simplistic thought of simply using digital tools to transform or copy. Of course, that’s one approach, but fundamentally speaking, if you’re using digital tools, it would be faster to create a perspective tool from the start.
One analog method that comes to mind is ‘measuring with a ruler.’ Since all lines extending from the center of the circle to the circumference are the same length, you can simply measure a straight line and extend it from VP towards CP by the same length.
Alternatively, you could use a compass. These methods are reliable.
Another option is a more freehand approach, such as imagining the circle in your mind.
You could also use your elbow as a pivot to simulate a compass. Or, you might use a mechanical pencil, pen, rubber, string, or even your finger to estimate the length.
Also, the position of the MP might be inferred from the canvas size using some rule, and at the very least, it might be possible to record and reuse some generic values.
This will be left for later (to be addressed in a different article).
Next, the idea arises that it might be possible through a geometric method. Honestly, as someone from a humanities background, I can’t think of a solid solution.
I considered that the diagonal length of a square is √2, approximately 1.41, but this doesn’t seem very practical.
Of course, there are methods to subdivide the square to approach 1.41, but this would probably be an emergency measure for situations where there is no ruler.
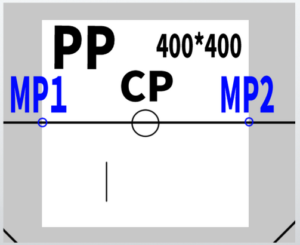
Using the ‘Depth Reference Point (DRP)’ to determine the depth
Now, with this, I understand how to slide the lines.
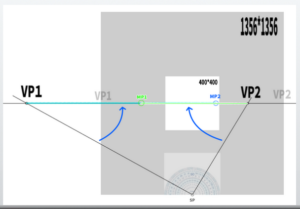
By sliding both the measuring point lines from VP1 to SP and VP2 to SP, we can discover two measuring points. Now, how do we use these to determine the depth?
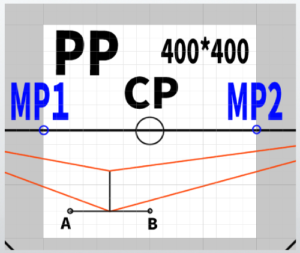
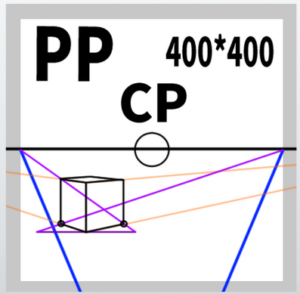
(1) draw an appropriate vertical line.
You just need to imagine the height of the cube you want to draw.
(2) Extend the vertices to VP1 and VP2, that is, to the original vanishing points.
Of course, at this stage, the depth is still unknown.
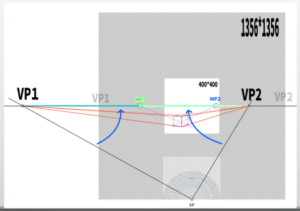
(3) Draw lines of the same length as the vertical line to the left and right
Using a ruler would likely be more accurate.
Since you are not converting diagonal lines into parallel ones, it might also be easier to draw freehand. Alternatively, extending the lines at a 45-degree angle will intersect each corresponding point. Label these vertices as A and B.
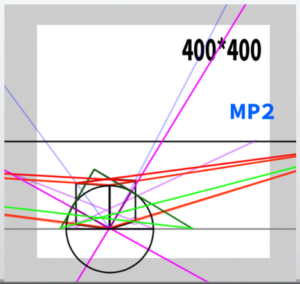
(4) Extend A toward MP2 and B toward MP1 so that they intersect
Label the point at the base of the initial vertical line as C. The intersection of the line extending from A to MP2 and the line extending from C to VP1 is the ‘point that determines depth.’ The same method applies for the opposite side.
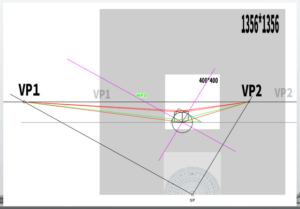
(5) All that remains is to complete the cube.
By extending lines from the ‘points that determine depth,’ the cube can be constructed.
Extend the remaining lines using the lines directed toward the VPs.
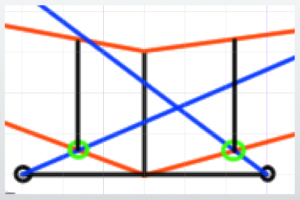
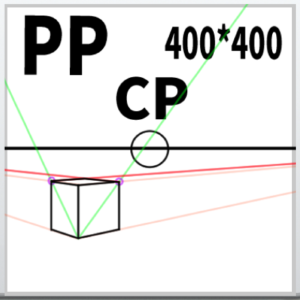
The completed cube
The completed cube is shown here, with almost no noticeable distortion.
The most crucial aspect of this method is determining the measuring points; once that is understood, the rest is straightforward.
Drawing a Cube Using the Medium Line Method
What is a medium line? Meaning, definition, and an easy-to-understand explanation
POINTMedium Line (ML): straight line converging at a 45-degree vanishing point.
The point at the end of the medium line is the 45-degree vanishing point, which can be considered a type of measuring point (auxiliary point). This point will be referred to as the ‘medium point’ (MDP) for distinction from the measuring point (MP).
First, this screen can be constructed using the knowledge from previous videos.
The main issue with the medium line method is ‘where the medium points determining the depth are located and how to establish them.’ If you have understood the ‘method of sliding along the circumference of a circle’ learned earlier in the measuring point method, it will be simple.
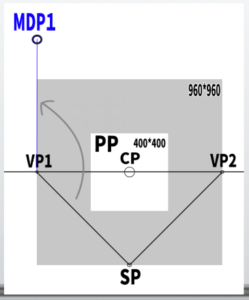
(1) Establish the Medium Point
Extend a vertical line from VP1 with the same length as the diagonal line from SP to VP1, and that point will be MDP1.
You can use a ruler or compass, or employ digital tools like transformations or copying. Of course, drawing intuitively is also fine.
If the length from VP1 to CP is considered as 1, the length is √2 (1.41). For a canvas size of 480 × 1.41 = 676.8, the canvas dimensions would be 1353×1353.
(2) Draw an arbitrary vertical line
Draw a vertical line corresponding to the height of the cube you want to create.
(3) Extend a line from the vertical line towards VP
(4) Extend a line from the point below the vertical line towards MDP
(5)The Depth Reference Point (DRP) is determined
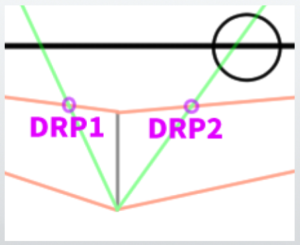 The point where the line extending towards VP intersects with the line extending towards MDP is the ‘depth reference point.’
The point where the line extending towards VP intersects with the line extending towards MDP is the ‘depth reference point.’
※This point, which determines the depth, will be abbreviated as ‘DRP’ (Depth Reference Point).
(6) After that, simply complete the cube
The completed cube
The completed cube is shown here. There isn’t much of a sense of incongruity. The difficulty seems to be quite similar to the measuring point method. However, it might require a larger workspace.
Do the Measuring Point Method and Medium Line Method Align?
Verification
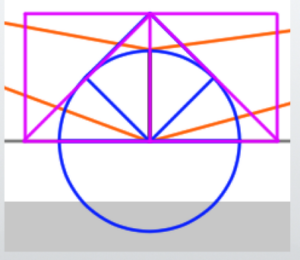
Now, a question arises. Do the Measuring Point Method and the Medium Line Method create the ‘same’ cube? Let’s examine this.
First, prepare the same length of perpendicular line used in the Medium Line Method. Then, here is the cube formed using the Measuring Point Method.
Let’s take another look at the cube formed using the Medium Line Method. It seems like a similar cube has been created.
Verification Results
When we overlay them, this is what it looks like. The conclusion from the verification is that the cubes created using the Measuring Point Method and the Medium Line Method match.
Drawing a Cube Using the Ground Line Method
What is a baseline? Meaning, definition, and an easy-to-understand explanation
First, let’s understand what the ground line is.
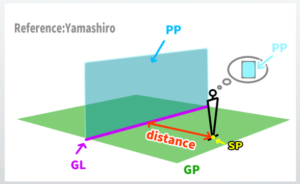
POINTGround Line (GL):The line where the base plane and the picture plane meet.
POINTGround Plane (GP):The plane where the object is placed and where the observer stands.
POINTPicture Plane (PP):The area that captures the field of view, typically in a rectangular shape.
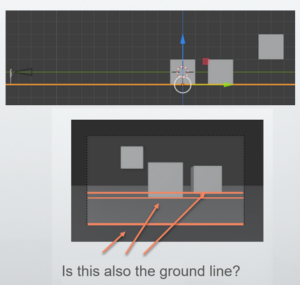
Where is the baseline located within the picture plane?
Even with this explanation, to be honest, I don’t quite understand. In such cases, I’ve heard it’s helpful to make a diagram.
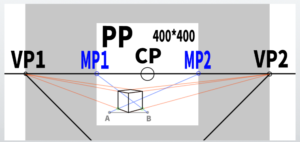
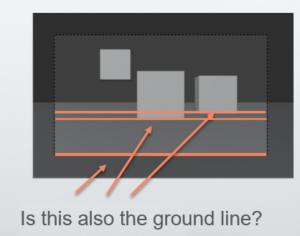
For example, let’s imagine a situation where three cubes are in front of us, as shown in the diagram on the right. Now, where is the ground line in the picture plane?
I have no idea. I don’t even understand if the GL (ground line) exists in a perspective drawing.
For example, if we look from the side as a plan view, this orange line is the ‘ground plane.’ If we look from above, this orange surface is the ‘ground plane.’ Specifically, it refers to the ground seen from the observer’s perspective.
Now, what does it mean for the ground plane and the picture plane to coincide?
For example, the image I showed first is the picture plane itself. Where does it coincide with the ground plane?
I thought the bottom of the PP was the ground line, that is, the GL. But is that really the case? Aren’t there many other points where the picture plane (PP) and the ground plane (GP) intersect?
For example, here and there, it can also be said that these are lines where the picture plane and ground plane intersect.
There should be no logical reason to say that the picture plane is only the frame. The picture plane should, after all, mean the whole, like a window.
In short, it may appear as a single line when viewed from the side, but from the front, there could be many, almost infinite ones.
Of course, since the Earth is round, it may not be a perfect straight line, but over short distances, it would almost be a straight line.
Drawing using the baseline method without a plan view
Now, the Ground Line Method is a perspective method that literally uses the ‘ground line.’ Previously, I distinguished between the point method and the medium line method, which do not use a plan view, and the foot line and ground line methods, which do use a plan view.
However, it seems that the ground line method might be possible even without a plan view (this may be because it’s a simple cube).
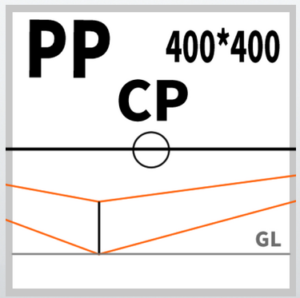
(1) Draw the vertical line of the cube you want to draw.
This can be any size, and you can decide the length. For verification purposes, I used the same position and length as those used in the point method and medium line method.
(2) Draw lines to each VP
(3) Draw the ground line
Assuming the cube is on the ground, draw a line through the frontmost vertex as the GL.
(4) Draw horizontal lines to the left and right with the same length as the vertical line you drew, forming a circle
To draw a circle accurately by hand, using a compass is likely the most effective method.
Let’s assume we’re using a compass here. If you don’t have a compass, one could create a square and approximate a circle, though this is a more tedious approach.
Since precision like that in architecture isn’t always required in drawing, it’s probably fine to draw intuitively.
Of course, in digital drawing, it’s best to use the circle tool. By the way, since you’ll only use the upper half of the circle, a semicircle would work fine.
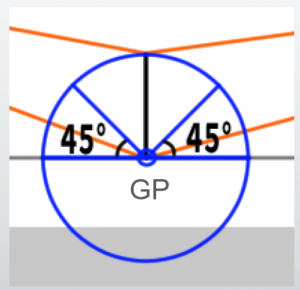
(5) Draw lines from the starting point to each VP, parallel to the line extending from SP to VP
This is likely the most difficult part to understand. In this case, we are dealing with a two-point perspective at 90 degrees, with equal left and right angles (45:45).
In other words, the lines extend at a 45-degree angle to the left and right. Therefore, you should draw lines at a 45-degree angle from the starting point to each VP.
When you actually extend the lines, it will look like this. If the angles were different, for example, 30°:60°, it might be difficult without a protractor. Alternatively, you might need to use a geometric method.
(6) Create a square based on the lines extended horizontally
This should be easy. Especially since this time it’s at a 45° angle, simply draw the diagonal lines to complete the square.
(7) Extend the sides of the square
Imagine creating a triangle, and extend the sides of the square like this to the GL.
Alternatively, it might be possible to imagine a larger square using the diagonal (√2).
By the way, if a fairly rough approximation is acceptable, there may be a shortcut method. With this method, there’s no need to draw a perfect circle.
For example, starting with the initial vertical line as 1, you could add 1/3 of that to create a square.
Of course, the actual measurement would be slightly larger. It’s probably around 1/3 + 1/12 (which is 1/4 of 1/3).
I just realized that 1/3 + 1/12 equals 5/12, which is approximately 0.41. In other words, the total is 1.41, almost the same value as √2 (the difference is about 0.0027).
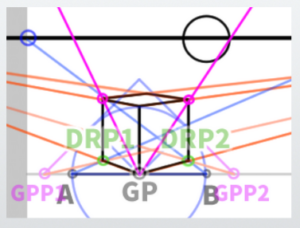
(8) Extend a line from the newly determined point to VP
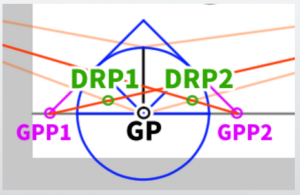
Let’s call the newly determined point the ‘Ground Plane Point (GPP)’. GPP1 will extend a line to VP2, and GPP2 will extend a line to VP1.
Extend lines from GPP to VP and from GP to VP, and the point where they intersect will be the ‘Depth Reference Point’ that determines the depth. This point will be referred to as ‘DRP’ for short.
(9) Complete the cube
After that, simply draw lines according to the DRP to complete the cube.
The completed cube
When only the cube is displayed, it looks like this.
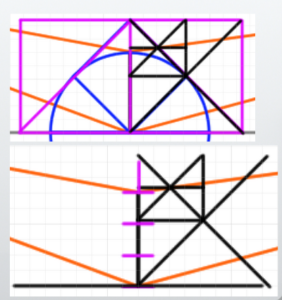
Do the “Measuring Point Method” and “Medium Line Method” Align with the Ground Line Method?
Verification Results
As shown in the diagram on the right, they match. No matter which method is used, the same cube can be created in this case.
Trying Other Cone of Vision and Angles
Try the 30:60 case
The perspective methods so far have mainly dealt with the case of a 90-degree cone of vision and a 45-degree equal distribution in two-point perspective.
This time, let’s work with an unequal case. For example, the case where the left is 30 degrees and the right is 60 degrees.
Create the initial screen
The canvas size will be set to a simple 400×400. For this time, we will use the case where the Cone of Vision covers the entire screen (the full case).
※Therefore, the formula is X (the side of the square) = √(width² + height²). When calculated, this gives 565. Multiplying this number by 2.4 (for a 45-degree Cone of Vision) gives 1356. For the reason why this calculation formula is necessary and why we must consider the Cone of Vision, please refer to the fourth video. There might be a simpler and more reasonable method, but for now, we will use this one.
[Fourth Session] What is the cone of vision (COV) in perspective?
When visualized, it looks like this. By drawing a line from the VP at a 90-degree angle, the SP is automatically determined (once the VP is determined, the SP is also decided, and vice versa). However, this will result in a 45-degree symmetrical perspective method, as is the case with the left and right.
How to distribute 30 degrees to the left and 60 degrees to the right
Now, what should be done when wanting to distribute 30 degrees to the left and 60 degrees to the right? This time, we will simply use a protractor.
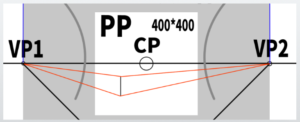
Try using the Measuring Point method
First, let’s try the measuring point method.
(1) First, slide the lines from SP to VP for each
(2) Then, follow the steps you’ve learned to form the cube
Let’s compare 45:45 and 30:60
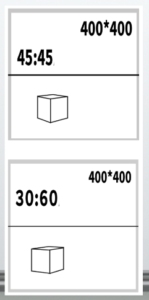 Comparing 45:45 and 30:60, a clear difference is noticeable. The 30:60 setup results in a larger range for the left face.
Comparing 45:45 and 30:60, a clear difference is noticeable. The 30:60 setup results in a larger range for the left face.
It is not easy to determine which is more aesthetically pleasing just from this.
If you want to emphasize the face, a larger face range would be better.
In other words, the way lower-level elements are arranged is determined by higher-level contexts, and the way those elements are positioned follows from that.
Verification with the medium line method
I’ve also checked to see if both the medium line method and the base point method yield the same result. First, here’s the medium line method.
Verification with the base point method
Here is the base point method. As expected, anything other than 45:45 seems a bit more troublesome to draw.
Verification results
It has been confirmed that no matter which method is used, the approximate positions match.
The measuring point method may be relatively easier. Other patterns that are not 90 degrees, such as 60:60 or 30:90, can also be applied.
In any case, the 90-degree pattern, especially 45:45, seems easier to create. However, it would be best to prioritize the angle you want to showcase and the most aesthetically pleasing angle.
Plans for the Next Session
I plan to explain what three-point perspective is.
References
Books that are easy for beginners to understand
David Chelsea「Extreme Perspective! For Artists: Learn the Secrets of Curvilinear, Cylindrical, Fisheye, Isometric, and Other Amazing Drawing Systems that Will Make Your Drawings Pop Off the Page 」
The book contains many illustrations and is easy to understand. It also explains basic perspective terminology and provides a simple explanation of how to use perspective. However, it is important to note that the book focuses on ‘illustration (manga)’ rather than architectural perspective.
It is suitable as the first book to pick up for learning the basics of perspective in general.
Robbie Lee「Perspective Made Easy: A Step-by-Step Guide」
Robbie Lee「Perspective Made Easy: A Step-by-Step Guide」
This is a suitable book to pick up as the first one for learning the basics of perspective in general.
I found it to be simpler and more detailed than ‘Perspective! Learn Perspective Through Manga.’ Therefore, I especially recommend this book to beginners as their first read.
Scott Robertson「How to Draw: drawing and sketching objects and environments from your imagination」
Scott Robertson「How to Draw: drawing and sketching objects and environments from your imagination」
A book specialized in drawing, particularly focused on line art. Though somewhat complex, it provides a broad and in-depth explanation.
About the Japanese version of this article
This article is a translation of an article written in [https://souzoulog.com/2024/12/26/basic-of-perspective-6/]. For detailed references, please refer to this link.














Comments