[Fifth Session] What is Two-Point Perspective? A Guide to the Basics

Introduction

Explanation in the video

The ‘Overview, Summary, or Conclusion’ of this article can be found at the beginning of the YouTube video, so please refer to it.

If possible, we would appreciate it if you could subscribe to our channel to help maintain the site. It serves as motivation for us!

An easy explanation of what two-point perspective is

What is Two-Point Perspective?

The way two-point perspective is expressed varies greatly depending on the position of the two vanishing points. Of course, understanding this concept requires more than just this simple definition.”

For example, the upper view uses one-point perspective, while the lower view uses two-point perspective. These represent the same cube viewed from different angles.

So, where does the ‘difference’ between these two lie?

Understanding this ‘difference’ is key to grasping two-point perspective and serves as the main purpose of this video.

First, we will identify the ‘differences’ that can be objectively observed, and finally, we will interpret the reasons behind them.

How Many Faces of the Cube at the Center of the Picture Plane Are Visible?

In one-point perspective, only one face is visible at the center of vision.

In two-point perspective, two faces are visible.

This is the primary difference between the two.

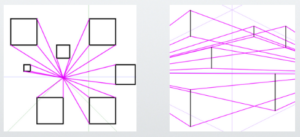
How many diagonal, vertical, and horizontal lines does the cube at the center of the picture plane have?

In one-point perspective, there are two horizontal lines, distinct from the horizon line, and two vertical lines.

In two-point perspective, there are three vertical lines and four diagonal lines.

Simply put, one-point perspective is made up of horizontal and vertical lines, while two-point perspective consists of vertical and diagonal lines.

How Are the Camera or Human Head Positioned?

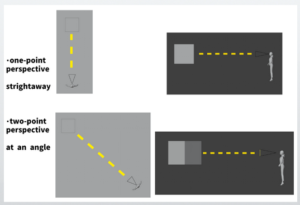
･Case Viewed from Above

In one-point perspective, they are facing the subject straight ahead.

In two-point perspective, they are facing the subject at an angle.

What Happens When You Tilt Your Head?

In both one-point and two-point perspective, the lines extended at perfect 90-degree angles.

This straight extension of lines indicates that the neck remains fixed without tilting up or down.

So, what happens when you tilt your head up or down?

Tilting your head refers to the action of moving your neck up or down.

For example, if your neck remains straight, it becomes difficult to look through a camera positioned this way. Therefore, tilting your head becomes necessary. You could also describe this as bending your neck.

Of course, you could tilt your entire body as if floating in space to look downward, but we’ll consider that an exception.

When you tilt your head, one of the resulting views is a case like this, which corresponds to what is known as three-point perspective. However, we will not be covering three-point perspective in this case.

Keep in mind that both one-point and two-point perspective represent views where the head is not tilted up or down, but rather looking straight ahead.

The Relationship Between Convergence and Perpendicular Lines

Converging Lines and Non-Converging Lines

Earlier, we reviewed the perpendicular lines, horizontal lines, and diagonal lines in both one-point and two-point perspective.

What do these lines actually represent?

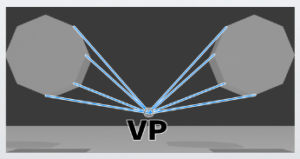
First, perpendicular lines and horizontal lines are essentially ‘lines that do not converge to a vanishing point.’

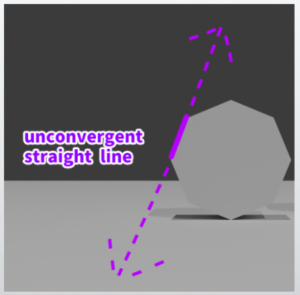
However, ‘just because a line is diagonal, it does not necessarily mean it will converge to a vanishing point.’

For example, as seen in the diagram on the right, the front of the octagon is filled with diagonal lines, but these diagonals, like the vertical and horizontal lines, do not converge to any point; they extend infinitely.

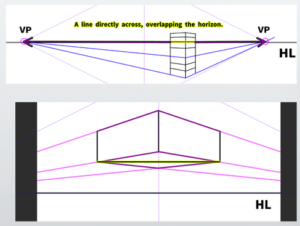
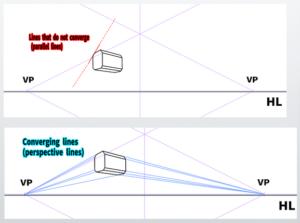
In two-point perspective, vertical and horizontal lines (lines that run directly horizontally) are generally ‘lines that do not converge to a vanishing point (non-perspective lines).’

However, it is important to reaffirm that there are lines that extend vertically or horizontally at a 90-degree angle (true vertical and true horizontal lines) in two-point perspective.

For example, true horizontal lines generally appear at the same level as the horizon line.

However, these true horizontal lines are ‘special lines that converge to a vanishing point (perspective lines).’ While non-perspective horizontal lines may exist in some cases, they are considered exceptions in two-point perspective.

Characteristics of Each Type of Perspective

1. In one-point perspective, the vertical and horizontal lines do not converge, only the lines in the depth direction converge to the vanishing point.
2.  In two-point perspective, the vertical lines do not converge, but the lines in the depth direction and horizontal direction converge to different vanishing points.
3. n three-point perspective, all lines, including vertical lines, converge to vanishing points.

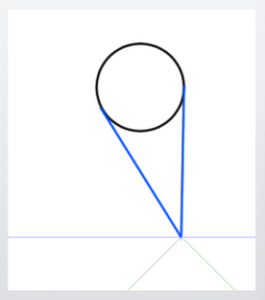
However, the diagonal lines and curves of shapes like stars or circles seen from the front need to be considered separately.

The converging diagonal lines are shown here. This is the case for one-point perspective, and the key point is that these are ‘lines in the depth direction.’

In one-point perspective, convergence due to perspective only occurs in the depth direction. In other words, diagonal lines in the depth direction are the converging lines.

In two-point perspective, and even in three-point perspective, these diagonal lines generally do not converge to any vanishing point.

Since these diagonal lines do not converge, curves obviously do not converge either. For example, drawing a sphere in two-point perspective is difficult.

Of course, it’s also difficult in three-point perspective. While it is possible to incorporate circles, as we learned last time, it results in an awkward sense of depth.

Let’s imagine a situation where we draw circles or stars and apply perspective to their depth. Initially, these circles or stars are not drawn using perspective. They are made possible through the act of drawing, using intuition (or geometry, etc.).

While depth lines (perspective lines) can certainly be extended, problems arise when trying to draw curves after extending them.

Two-Point Perspective as a Guideline

Of course, it’s possible to use perspective as a guideline, that is, as a rough reference for size and depth. Additionally, there are often explanations of perspective specifically focused on creating guide lines for drawing circles accurately.

However, if you want to represent a strict sphere in a two-dimensional drawing with precise perspective, using 3D software is preferable. For example, industrial products often require such software, and even in analog methods, geometric knowledge would be necessary.

In analog drawing, the skill to construct a sphere from a cube by your own effort, using ‘drawing ability,’ is essential. For beginners, it’s generally best to focus on being able to construct a cube from scratch using one- to three-point perspective.

In some cases, this alone may be a sufficient goal. This is because, with solid drawing skills, you can construct a sphere from the sense of size and depth of the cube, and then build a face from that sphere.

It’s not always practical to strictly draw everything you want with perspective. The reason perspective is crucial in architecture is likely because there are few curves involved.

In any case, architecture uses specialized software, making it a slightly different case from drawing in general.

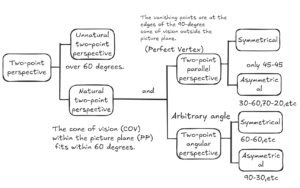
Types of Two-Point Perspective

There are many types of two-point perspective

How many types of two-point perspective are there? The answer is ‘many.’

The position of the left and right vanishing points, as well as the height of the viewer’s eyes, can result in many variations of two-point perspective.

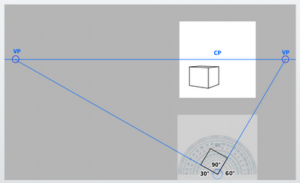
For example, two-point perspective at 45 degrees to the left and right is different from two-point perspective with 30 degrees to the left and 60 degrees to the right.

Additionally, even with the same 45-degree angle, changing the eye level from 50 cm to 60 cm will create different types of perspective (resulting in different views).

However, although there are infinitely many variations, it is possible to categorize them into a few types.

For example, based on the requirement to fit within a natural cone of vision, we can divide two-point perspective into two types: natural two-point perspective and unnatural two-point perspective.

Additionally, we learned previously that a natural two-point perspective, which is less prone to distortion, has a cone of vision within 60 degrees.

The vanishing points are typically located outside the picture plane, and we can distinguish between different types of two-point perspective based on whether the vanishing points are positioned at the edges of the 90-degree cone of vision (the left and right extremes of the cone) or at other angles.

When summarized, the diagram looks like this. For information on the cone of vision, please refer to the previous video.

What is a Perfect Vertex? Definition, Meaning, and a Simple Explanation

The most common type of two-point perspective is the 45-degree vanishing point method, known as Two-Point Parallel Perspective.

This corresponds to what Robbie Lee refers to as the Perfect Vertex. It is widely used, likely because it is easier to construct.

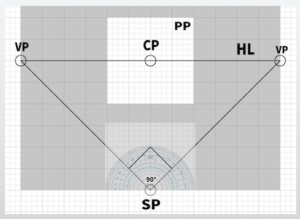
In two-point perspective, when the two vanishing points are symmetrically positioned, both the Perfect Vertex and the vanishing points are equidistant from the center of vision.

Extend lines from the station point (SP) to the left and right vanishing points, imagining these three points forming a right triangle.

A right triangle is defined as a triangle where one of the three interior angles is 90 degrees.

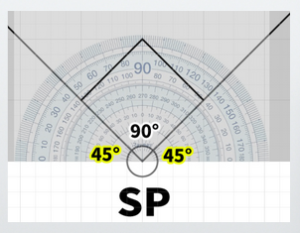
The reason it can be called 45 degrees is that the diagonal vanishing points are each located at a 45-degree angle from the station point (SP).

This concept may seem a bit tricky, but essentially, it refers to the fact that the lines extending toward the vanishing points form a 45-degree angle.

Note: The sum of a triangle’s interior angles is 180 degrees, so (180 – 90) / 2 = 45. You can imagine this using a protractor.

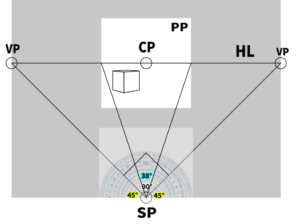
The Relationship Between a Natural Picture Plane and a 90-Degree Cone of Vision

Note that being 45 degrees does not necessarily mean that the cone of vision within the picture plane is limited to 45 degrees.

For instance, in the diagram on the right, the cone of vision is approximately 38 degrees. The key point here is not ‘what cone of vision the picture plane fits into,’ but rather ‘at what angle the vanishing points are located relative to the SP.’

Cases of Unequal Right Triangles

Additionally, there are both symmetrical and asymmetrical cases.

For example, a configuration with 30 degrees to the left and 60 degrees to the right represents an asymmetrical, non-equidistant setup, yet still forms a right triangle.

The key point here is that such cases can still be constructed relatively easily, even analogically, with a right-angle ruler.

The appearance of each square differs as shown here.

It ultimately comes down to the creator’s skill to choose which presentation or visual impact they wish to achieve.

The Relationship Between Artistic Sense and Perspective

The indicators of ‘distorted’ or ‘undistorted’ are not clearly defined in this context; it may be more of a matter of sense or intuition.

For example, most photographs taken by photographers are not distorted (thanks to camera adjustments that naturally minimize distortion), yet there are beautiful and unattractive photographs.

In a way, this relates to the issue of composition. The choice of composition depends on the purpose.

For instance, if the goal is to express ‘the grandeur of a mountain,’ one might choose a composition that feels like looking up from below. Various such cases can be considered.

Advantages and Disadvantages of Two-Point Perspective

What Are the Benefits of Two-Point Perspective? Meaning, Definition, and Easy Explanation

1. It allows you to depict scenes that cannot be represented with one-point perspective. Specifically, you can “view” the subject from an “angled” position.
2. It appears more dynamic compared to one-point perspective.
3. Since the “degree of receding lines” is more gradual than in one-point perspective, it can result in a convincing outcome even without precise drafting.

What Are the Drawbacks of Two-Point Perspective? Meaning, Definition, and Easy Explanation

1. Drafting is challenging and time-consuming.
2. The “frontal emphasis” achievable with one-point perspective is lost, making it harder to discern the subject’s exact shape.
3. While one-point perspective allows for “simple, clear, and impactful drawings,” two-point perspective tends to be more complex.

If you were a photographer, what would you want to show?

The important thing is to ask yourself, ‘As a photographer, how do I want the viewer to perceive the subject before me?‘

When drawing, you are essentially a photographer capturing and framing your imagined world.

For instance, how would you choose to present this simple cube? What purpose does your chosen perspective serve, and what effect does it create?

Now, imagine applying this thought process to something like a human face—it becomes even clearer. Perspective techniques provide you with options, but they don’t dictate the right choice.

Next Session Preview

Learn how to construct a cube using two-point perspective.

References

Books that are easy for beginners to understand

David Chelsea「Extreme Perspective! For Artists: Learn the Secrets of Curvilinear, Cylindrical, Fisheye, Isometric, and Other Amazing Drawing Systems that Will Make Your Drawings Pop Off the Page 」

David Chelsea「Extreme Perspective! For Artists: Learn the Secrets of Curvilinear, Cylindrical, Fisheye, Isometric, and Other Amazing Drawing Systems that Will Make Your Drawings Pop Off the Page 」

The book contains many illustrations and is easy to understand. It also explains basic perspective terminology and provides a simple explanation of how to use perspective. However, it is important to note that the book focuses on ‘illustration (manga)’ rather than architectural perspective.

It is suitable as the first book to pick up for learning the basics of perspective in general.

Robbie Lee「Perspective Made Easy: A Step-by-Step Guide」

Robbie Lee「Perspective Made Easy: A Step-by-Step Guide」

This is a suitable book to pick up as the first one for learning the basics of perspective in general.

I found it to be simpler and more detailed than ‘Perspective! Learn Perspective Through Manga.’ Therefore, I especially recommend this book to beginners as their first read.

Scott Robertson「How to Draw: drawing and sketching objects and environments from your imagination」

Scott Robertson「How to Draw: drawing and sketching objects and environments from your imagination」

A book specialized in drawing, particularly focused on line art. Though somewhat complex, it provides a broad and in-depth explanation.

About the Japanese version of this article

This article is a translation of an article written in [https://souzoulog.com/2024/12/01/basic-of-perspective-5/]. For detailed references, please refer to this link.