[Fourth Session] What is the cone of vision (COV) in perspective?

Introduction

Explanation in the video

The ‘Overview, Summary, or Conclusion’ of this article can be found at the beginning of the YouTube video, so please refer to it.

If possible, we would appreciate it if you could subscribe to our channel to help maintain the site. It serves as motivation for us!

Understanding the Cone of Vision in Perspective

The Difference Between Field of View and Cone of Vision

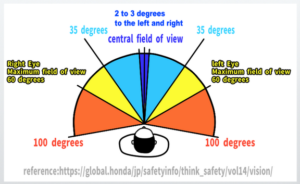
What is field of view? Meaning, definition, and a clear explanation

As explained in the previous video (the third one), we can think of the screen as being divided into a large field of vision and a specific canvas (finder).

What is field of view? Meaning, definition, and a clear explanation

The large field of vision does not fundamentally overlap with the entire range that can be seen naturally.

In other words, it includes the concept of areas that appear unnatural, blurry, or distorted at the periphery.

It is said that the maximum field of view for humans is around 100 degrees, while the effective field of view is approximately 35 degrees to the left and right.

This so-called effective field of view is near the boundary of the area that appears natural.

In the world of perspective, it is said to be around 30 degrees to the left and right (with a cone of vision of 60 degrees).

What is a cone of vision? Meaning, definition, and a clear explanation

It represents the visual field depicted by line art. It can also be treated synonymously with field of view.

In essence, the cone of vision is an angular representation of the range within the field of vision or field of view where humans perceive things as particularly natural, further illustrated in the shape of a cone.

A specific canvas needs to be constructed to align as closely as possible with this naturally visible range of vision.

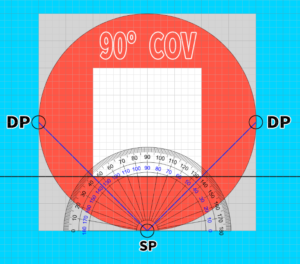
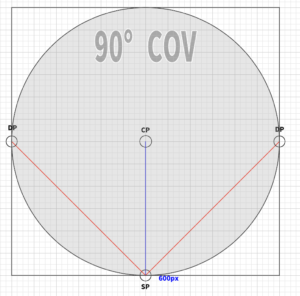
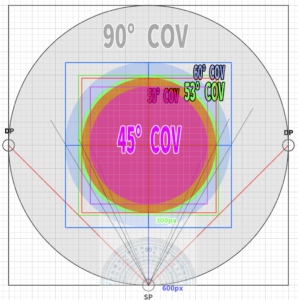
For example, the cone of vision with a 90-degree angle, using a diagonal distance point (DP) created previously at 45 degrees, can be illustrated in this way.

It extends 45 degrees to the left and right, making it 180 – (45*2) = 90 degrees, which means it is a cone of vision of 90 degrees.

Clarification on Misunderstandings from the Previous Video

Is the length of the width in simple proportion to the size of the cone of vision?

This time, I would like to delve into the points where I felt something was wrong, but I didn’t quite understand where the mistakes were.

I considered deleting the entire previous video, but since my videos are not a course that presents only correct answers, but rather a “history of understanding (log),”

I believe that mistakes can also lead to success. It should also help others who might make the same mistakes as I did.

In my understanding, with a square canvas, I believed that half the width of the vanishing point along the diagonal at 45 degrees would perfectly fit within the cone of vision of 45 degrees.

In other words, I thought that the length of the width was proportional to the size of the cone of vision. For example, if a width of 800 forms a 90-degree cone of vision, then a width of 400 would form a 45-degree cone of vision. This is where my misunderstanding lies.

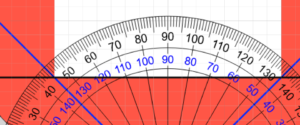
However, when I actually used a protractor to draw the lines, I realized that the cone of vision does not measure 45 degrees.

I had experimented with the same thing a long time ago, but it seems I conveniently interpreted the results by assuming that the protractor was simply not matching up.

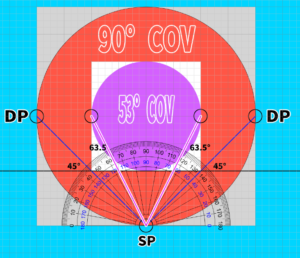
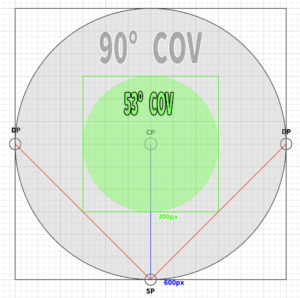
The actual cone of vision is approximately 53 degrees, not 45 degrees

The actual data obtained was approximately 63.5 degrees.

So, 180 – (63.5 * 2) = 53, meaning that a cone of vision of about 53 degrees overlaps with a 400 * 400 canvas.

When illustrated, it looks like this.

Of course, since the cone of vision generally experiences minimal distortion when it is less than 60 degrees, this is not a significant issue.

In fact, when creating a cube, no major distortions were observed.

However, in one-point perspective, it is often recommended to have a cone of vision between 40 and 50 degrees, so the slightly larger angle becomes a personal concern for me.

In this article, I will explore whether there is a way for a 45-degree cone of vision (as well as 50 and 60 degrees) to perfectly align with this 400 * 400 screen.

Finding the Position Where a 45-Degree Cone of Vision Fits on the Screen

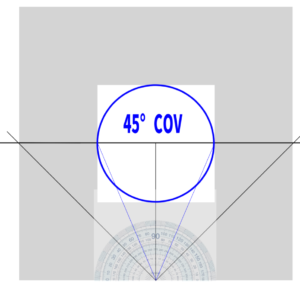
Where is the 45-degree cone of vision located?

I created the 45-degree cone of vision using a protractor to see where it might be positioned.

How can we ensure that this green circle fits perfectly within the screen (the white area)?

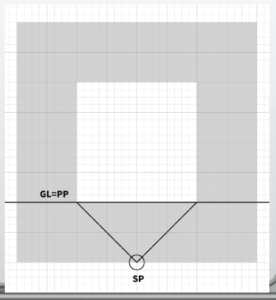
In the previous article, I determined the position of the SP(station point) by extending lines at a 45-degree angle from the equal position of the GL (ground line) and PP (picture plane).

From there, I extended the lines to find the vanishing point of the diagonal. However, that does not mean the position of the diagonal vanishing point from the previous video was incorrect.

The position of the diagonal vanishing point is accurate, and if the goal is to use it to draw a distortion-free cube, then it has been approximately successful.

Consider it from the viewpoint of the vanishing point, rather than the screen (PP)

Let’s change our perspective slightly and reconsider things. In the previous video, I determined the position of the station point based on the size of the canvas.

This time, I will freely decide the position of the station point.

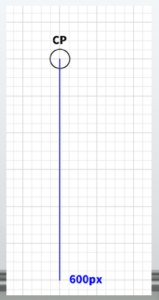
First, let’s consider the distance from the center of perspective (CP,Center of Vision). I will arbitrarily set this distance to 600 pixels for this example.

So, it will look like this. The key point is that I have not yet determined the size of the screen (PP).

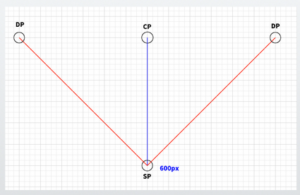
Once the 45-degree cone of vision is created, we can simply create the screen there.

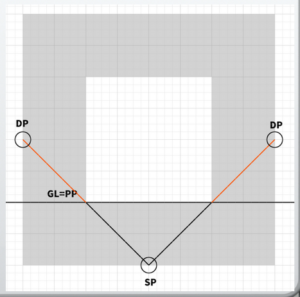
The position of the diagonal vanishing point (DP) is determined by the distance from the center of perspective (CP) to the station point (SP).

By extending a line at 45 degrees from the station point (SP), the position where it overlaps with the line of the center of perspective (CP), or the line of eye level (IL), becomes the diagonal vanishing point (DP).

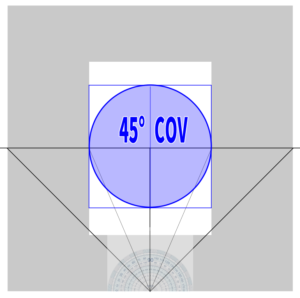
By using the position of the diagonal vanishing point (DP) from the center of perspective (CP) or the position of the station point (SP) as a reference, I can create a square and draw a circle inside it to form a 90-degree cone of vision.

Next, it is necessary to fit the screen appropriately within the field of view, that is, inside the cone of vision.

As previously calculated, by halving the distance from the center of perspective (CP) to the station point (SP), a cone of vision of approximately 53 degrees is formed.

However, this time we want to create a screen that goes beyond just half that distance. Moreover, we aim to create a screen (canvas) that perfectly fits within a 45-degree cone of vision.

(1) Method for constructing the screen using a protractor

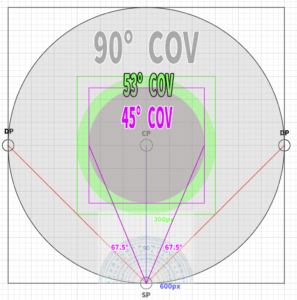
【1】First, there is a straightforward method using a protractor. By extending lines at 67.5 degrees to the left and right from the station point (SP) along the line of eye level (IL), we can create a 45-degree cone of vision.

Once this is done, we can later set a square screen that covers this cone. For example, we can set the canvas to 500 * 500 pixels from this point.

Method for constructing the screen using canvas size

【2】Looking for Methods Other than Using a Protractor

1. The distance from the center of perspective (CP) to the station point (SP) is 600.
2. A 90-degree cone of vision is 1200 * 1200.
3. A 53-degree cone of vision is 600 * 600.
4. A 45-degree cone of vision is 500 * 500.

*Note: The numbers are approximate and not exact.

If we want to perfectly fit the canvas size within the diagonal vanishing point of 45 degrees, what can we do?

One possible idea is to “extend the distance of the station point (SP).” In other words, this means adjusting the position of the diagonal vanishing point (DP) instead of the picture plane (PP).

When the picture plane (PP) is 500 * 500, the diagonal vanishing point (DP) comes to a position of 1200. This means we can assume it is approximately 2.4 times farther away.

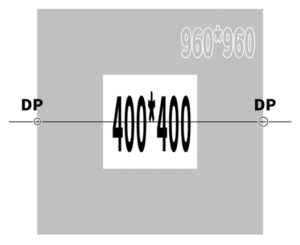
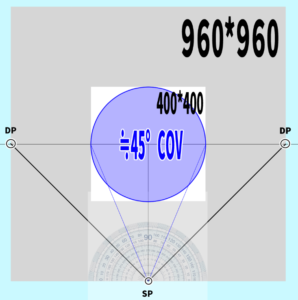
Applying this rule, if the picture plane is 400 * 400, we can estimate that the diagonal vanishing point (DP) will be at a position of 400 * 2.4 = 960.

Example: How to create a 45° cone of vision within a 400×400 canvas

Let’s try creating it. First, we will make a canvas of 400 * 400.

Next, we will create a 960 * 960 square and use that as the diagonal vanishing point (DP).

We will measure whether this picture plane (PP) of 400 * 400 fits perfectly within the 45-degree cone of vision using a protractor.

As a result, it aligned closely with the line at 67.5 degrees on either side (some margin of error may exist). This means it fits within the 45-degree cone of vision.

180 – (67.5 * 2) = 45

To summarize, for square canvases:

・45-degree DP = H or W × 2.4

・53-degree DP = H or W × 2

Additionally, we will derive formulas for other angles that may be versatile, such as 40 degrees, 50 degrees, and possibly 60 degrees, which might not be commonly used in one-point perspective.

Note: H refers to height and W refers to width. These formulas are for generating any cone of vision that fits within a perfect circle inside a specific square canvas.

Finding the Position Where a 50-Degree Cone of Vision Fits on the Screen

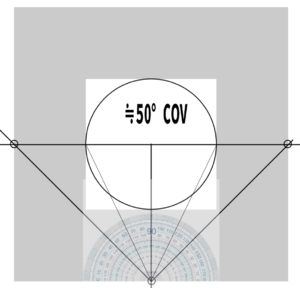
Find the formula to construct a 50° cone of vision

The 50-degree cone of vision is approximately 576 * 576. Therefore, 1200 / 576 = 2.083… We round it up to 2.1, as strict precision in units is generally not necessary unless in architecture.

For square canvases, 50-degree DP = H or W × 2.1.

Assuming 50-degree DP = H or W × 2.1, we will construct the screen. Let’s set H (or W) to 400. Calculating gives approximately 840. We will set DP at this position.

This brings it to a roughly correct position, meaning the 50-degree cone of vision aligns with the screen (around 65 degrees left and right).

Finding the Position Where a 60-Degree Cone of Vision Fits on the Screen

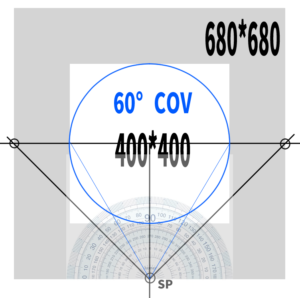
Find the formula to construct a 60° cone of vision

For 60 degrees, it was approximately 710*710.

Therefore, 1200/710=1.69… and we will round it up to 1.7.

In the case of a square canvas, 60-degree DP=H or W×1.7.

Here is the image illustration.

For 60 degrees, DP = H or W × 1.7, and setting H to 400 gives approximately 680.

This position sets DP at roughly the correct location, meaning the 60-degree cone of vision aligns with the screen (about 60 degrees left and right).

Finding the Calculation Formula for Rectangular Screens

Review of the previous session

Now, the question is whether these formulas also apply to a “rectangle.” The previously derived formulas are as follows:

1. If the height is greater than the width, then DP = 2W + (H – W).
2. If the width is greater than the height, then DP = 2H + (W – H).

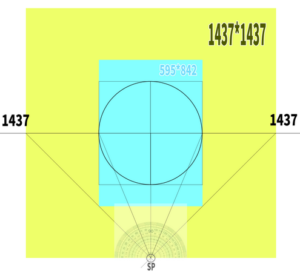
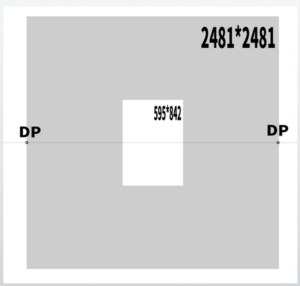
Let’s demonstrate this with an A4 size example. It is a canvas measuring 595 (width) * 842 (height).

Using the formula DP = 2W + (H – W), we find DP = 2(595) + (842 – 595), which equals 1437.

When using a protractor to draw, it turns out that we arrive at a position for the visual cone that is surprisingly close to 45 degrees.

Since 1437 / 595 = 2.41, this approximates the 2.4 times formula. I might have misunderstood this calculation result before.

The reason for this phenomenon will not be considered here, but various factors, such as the ratio of height to width, might be involved.

However, there are tricky elements lurking in the visual cone of this rectangle. In short, the question is, “Is the visual cone elliptical?”

Due to the properties of the cone of vision, wouldn’t it fit within a square?

Given the properties of the visual cone, it seems that it should fit within a square.

Therefore, we can speculate that the actual visual cone would look something like this. It would be a different case if we could construct an elliptical visual cone, but that is not the scenario we are considering this time.

Consider methods to include more of the picture plane within a 45-degree cone of vision

If we want to fit everything within a 45-degree visual cone, it may be necessary to use a slightly larger visual cone.

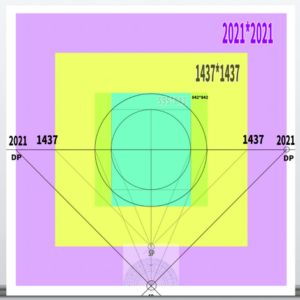
For example, what adjustments are needed to ensure that an area of 842*842 fits entirely within a 45-degree visual cone?

・45-degrees DP = H or W × 2.4.

Therefore, in the case of 842*842, DP should be at the position of 2020.8. Let’s round it to 2021.

When illustrated, it looks like this.

Of course, if you want to completely fill the A4 size from corner to corner, a slightly larger visual cone would be necessary.

This issue also applies to the square canvas size we discussed earlier. In other words, if you want to ensure that the edges are firmly contained within the 45-degree visual cone, a different calculation formula will be required.

While the distortion is likely to be negligible when drawing, there may still be some who are concerned about it.

Additionally, if you lower the viewpoint (SP) to compensate for this distortion, effectively enlarging the 45-degree visual cone itself, you may encounter a different sense of discomfort that isn’t related to distortion (giving a feeling of distance).

Consider methods to fit the entire picture plane within a 45-degree cone of vision

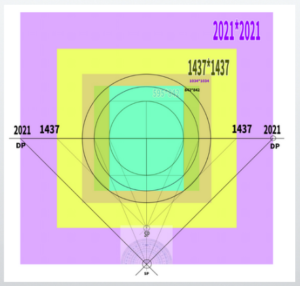
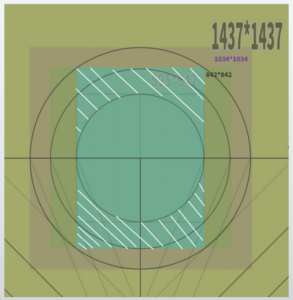
For example, considering a 1034*1034 perspective cone, it fits perfectly.

To make this perspective cone 45 degrees, it is necessary to move the vanishing point of the diagonal again.

・45-degrees DP = H or W × 2.4.

Therefore, the DP will be at the position of 1034 * 2.4 = 2481.6.

Finding the Calculation Formulas for Partial and Whole Cases

Two options

If you want to fit an A4-sized screen of 595 (width) * 842 (height) into a 45-degree visual cone, there are two options:

1. The case where the entire screen is contained within the 45-degree visual cone
2. The case where only a part of the screen is contained within the 45-degree visual cone

If you choose option (1), you need to consider a perfect circle that completely fits the A4 size. Then, imagine a square that can contain that perfect circle.

You just need to determine the position of the diagonal vanishing point from that square.

Formula for the whole case

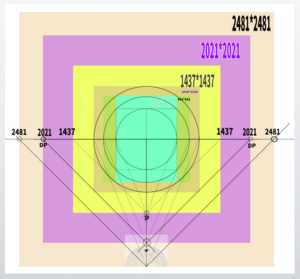
In mathematical terms, it can be expressed as follows. Let the length of a side of the square that can contain the perfect circle be X.

X = √(width² + height²)

For example, in the case of A4, X = √(595² + 842²). If you type “√(595^2 + 842^2)=” into Google, the calculation result will come back immediately. The result is 1031. What I visually estimated to be 1034 earlier is actually 1031. The symbol √ is read as “root.” The ^2 means “squared.” For this case, we will use 1034 as it is.

Example: ‘Whole’ pattern for A4 size

・45-degree DP = H or W × 2.4

Next, you should multiply that X × 2.4. Since X = 1034, then 1034 × 2.4 = 2481.6.

You should create a canvas of 2481 × 2481, using this canvas as the reference.

You can also round it up to 2482 if you prefer.

All that’s left is to set the vanishing point of the diagonal.

I actually drew a cube, and I didn’t notice any distortion.

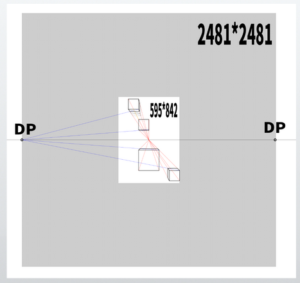
Returning to the original drawing screen, it looks like this.

Case of fitting a portion of the screen into a 45-degree cone of vision

(2) Case of fitting a part of the screen within a 45-degree view frustum

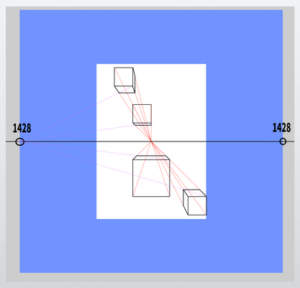
Now, let’s consider the case where only the square of the maximum width edge is fitted.

In the case of A4 size 595 (width) * 842 (height), a 595 * 595 square fits within the 45-degree view frustum, while anything outside of this will extend beyond the boundaries.

In the diagram, the area represented by the white diagonal lines falls outside the range of the 45-degree view frustum.

・45-degree DP = H or W × 2.4

Applying the formula, we have 595 × 2.4 = 1428. Using this diagonal vanishing point, I attempted to draw a cube in the same manner as before.

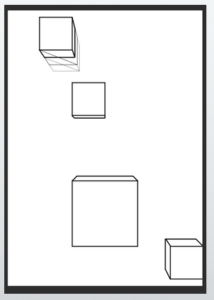
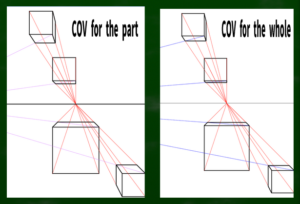
Comparing the distortion of the cube in the case of parts and the case of the whole

Indeed, when compared, it seems that fitting the entire screen neatly into a 45-degree cone of vision looks better.

In particular, the edges appear to make the cube look slightly elongated.

It’s not an overwhelming sense of discomfort, but it is a bit noticeable.

The overall case feels somewhat shorter, but this kind of perception should be honed by observing real objects. This is closely related to artistic sensibility.

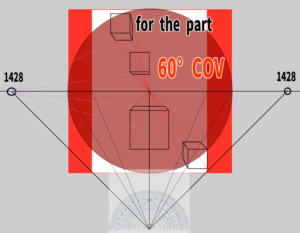
By the way, how much of the cone of vision extends beyond the partial area?

This area corresponds to about a 60-degree cone of vision, so we can say that most of it fits within the 60-degree cone.

Once it starts exceeding this cone, it surpasses 60 degrees, and the distortion becomes more pronounced.

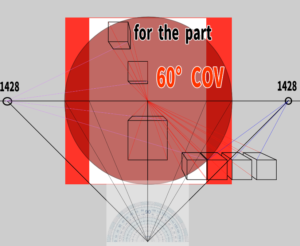
For example, if you draw a square in this area, it will likely appear distorted.

After all, with one-point perspective, it might be safer to fit everything into a 45-degree or 50-degree cone of vision rather than just a part of it.

With two-point or three-point perspective, even a 60-degree cone seems to work well.

Although there’s no absolute ‘correct’ way in art, it’s rare to draw something you want to emphasize in such a corner. If we assume the center will look more vivid, we might consider this a necessary compromise.

What Should Be the Degrees of the Cones of Vision for One-Point, Two-Point, and Three-Point Perspective?

What degree should the appropriate cone of vision be in the case of one-point perspective?

According to Scott Robertson, the following angles provide a more natural image:

【1】For one-point perspective: Keep the cone of vision within 40 to 50 degrees. If the cone of vision is too narrow, it will start to resemble the effect of a telephoto lens.

What degree should the appropriate cone of vision be in the case of two-point perspective?

【2】For two-point perspective:

Keep the cone of vision within 60 degrees.

However, since distortion increases towards the edges, it’s best to avoid placing important elements at the periphery.

Typically, a 60-degree cone of vision is commonly used for this type of perspective.

What degree should the appropriate cone of vision be in the case of three-point perspective?

【3】For three-point perspective:

Keep the cone of vision within 60 degrees.

The explanations for two-point and three-point perspectives will be covered in a separate article.

What Do We Gain by Sacrificing Distortion?

How much do you want to include in the drawing, and to what extent are you willing to accept distortion?

Robbie Lee states that the position of the DP (distance point) depends on “how much you want to include in the drawing and how much distortion you’re willing to tolerate.”

Create a natural screen using the value of two-thirds

However, in most cases, “it works well if you place the vanishing point about two-thirds of the screen’s width from the edge.”

For example, in the case of 400*400, the DP would be at the edge of a canvas size of DP = 400 + (400 * 2/3) * 2. This gives approximately 933.

When I actually created it, it resulted in an approximately 45-degree field of view.

With more precise drafting, it seems possible to achieve an exact value, but it’s fair to say that the range is roughly between 44 and 46 degrees.

This calculation is also close to the 45-degree DP = H or W × 2.4 formula, which in this case would yield 960, a difference of 27 from 933.

Now, can this method be applied to an A4 size as well?

Let’s calculate using the width of 595 for a 595*842 canvas.

Since DP = W + (W * 2/3) * 2, the result is approximately 1388.3.

When illustrated, it seems to fall within the 44 to 46-degree range, meaning it fits roughly within a 45-degree cone of vision.

However, this applies to the ‘partial’ case for the A4 size. The edges will exceed the 45-degree limit.

However, this does not immediately mean that the drawing will look unnatural.

If the edges are still approximately within 60 degrees, they will not create an excessively unnatural appearance.

As Lee stated, we should prioritize ‘how much distortion we are willing to accept.’

Consider whether it is merely a problem of distortion or a relationship between distortion and field of view

In the first place, if it were merely a matter of distortion, there would be no need for us to intentionally adopt a wide viewing cone.

It would be better to position the DP so that the entire screen fits within a 45-degree or 50-degree viewing cone.

For instance, one could calculate a circle using X = √(width² + height²).

However, unfortunately, the issue of setting the viewing cone is not just about distortion.

If we try too hard to correct the distortion, other aspects may negatively impact aesthetics or practicality.

In the case of A4 size, calculations indicate that a canvas size of 1031 should be used as a standard.

If using Lobby Lee’s calculation method, the DP should be positioned at 2405, calculated as DP = W + (W * 2/3) * 2.

If using a factor of 2.4, it would be 2474.

The issue of the visual cone can be described as a matter of “the relationship between distortion and field of view.”

If we reduce the field of view in an attempt to minimize distortion, our visual range also becomes limited.

For example, if there are 10 objects in front of us, a 45-degree visual cone may only allow us to depict 5 of them, while a 60-degree visual cone may allow for more.

Additionally, simply moving the SP (station point) further away from the objects can indeed allow for a broader range to be captured, but at the expense of being able to see the details more closely.

The appropriate range of the visual cone and the position of the station point when drawing is more complicated than one might imagine, and it can be said that there is no absolute answer to this issue.

It can only be said that cases with obvious distortion are undesirable, unless, of course, the intention is to create distortion deliberately.

In a natural range, various aspects such as how much distortion to allow, how much roughness in the artwork is acceptable, and how many elements to include are all tested against the creator’s sense of aesthetics.

It is a domain woven from experience and knowledge. One cannot arrogantly claim a definitive answer. What’s important is to assist the creator in achieving the composition they envision.

For example, imagine you are a photographer trying to fit all the students in front of you into the viewfinder

For example, if you are a photographer wanting to capture all the students in front of you in the viewfinder, you would zoom out if they don’t fit in the frame.

If you’re too far away, you’d zoom in. If you’re too close, you’d need to step back, and if you’re too far, you’d move closer. This way, you adjust the distance and field of view.

For example, if there are only three students, this composition would be acceptable.

However, it seems that there are more students present. Let’s try to address this by zooming out the camera.

Zooming out essentially means widening the field of view, which enlarges the visual cone.

To fit all 11 students (the cube) into the viewfinder, the field of view needed to be adjusted from about 40 degrees to 104 degrees.

Naturally, the edges will distort as a result.

You might think there isn’t much distortion. However, this is only because the cubes are overlapping, which softens the distortion.

When you increase the distance, the distortion becomes more apparent.

Now, in order to fit all ten people without expanding the viewing cone, the viewpoint must be moved.

This means the photographer needs to step back. I moved back about 50 meters along the y-axis.

Alternatively, it is possible to physically reduce the scale of the students, although this is practically difficult.

Another option might be to change their arrangement, such as creating a tiered stage to gather them together and achieve an angle that minimizes distortion.

There are various options for fitting them into the frame without stepping back or widening the field of view.

As a result of the photographer moving back, the image obtained shows that the distortion on the right side has been eliminated.

However, the objects appear smaller, making the individual facial expressions of the students likely less visible.

The difference between lowering the standing point (SP) and keeping the SP the same while widening the field of view lies in whether there is distortion.

Both methods generally create a dull and distant appearance in the overall image.

Both have a 40-degree visual cone, but the position of the standing point (SP) is closer on the left and farther on the right.

When the size of the screen is specified in production, it can be a dilemma. One option is to enlarge the image on the right to match the size of the left cube, though this can be challenging if such a large image cannot be displayed side by side, so only part of it is arranged.

It’s more of a composition problem than a drawing problem

We are primarily faced with these four options:

1. Enclose a large, vibrant portion (natural screen).
2. Enclose a small, dull entirety (natural screen).
3. Enclose a small, dull entirety (unnatural screen).
4. Structure the screen to enclose a large, vibrant whole.

Such issues are more related to composition than to drawing itself. They are fundamentally tied to the core artistic question of what constitutes appropriate screen composition and structure.

Finding a way to enclose the entire scene in a large, vibrant manner is challenging. While there may be methods like enlarging a screen that captures a small, dull entirety, I still struggle to visualize an effective composition.

Certainly, it may appear to be of a similar size. However, when a painting is too large, we often find it difficult to perceive all elements correctly and aesthetically at once. Beauty is largely about balance.

When taking photographs, there are significant limitations (for example, mountains cannot be moved).

However, for those who create objects freely in a painting, there is the freedom and dilemma of determining how many objects to place in an appropriate frame without forcibly expanding the canvas.

This is an issue that should be considered at the design stage (rough sketch) rather than simply zooming in or out on an already drawn picture.

List of Functions to Determine the Vanishing Point of Diagonals (Please bookmark this)

References

Books that are easy for beginners to understand

David Chelsea「Extreme Perspective! For Artists: Learn the Secrets of Curvilinear, Cylindrical, Fisheye, Isometric, and Other Amazing Drawing Systems that Will Make Your Drawings Pop Off the Page 」

David Chelsea「Extreme Perspective! For Artists: Learn the Secrets of Curvilinear, Cylindrical, Fisheye, Isometric, and Other Amazing Drawing Systems that Will Make Your Drawings Pop Off the Page 」

The book contains many illustrations and is easy to understand. It also explains basic perspective terminology and provides a simple explanation of how to use perspective. However, it is important to note that the book focuses on ‘illustration (manga)’ rather than architectural perspective.

It is suitable as the first book to pick up for learning the basics of perspective in general.

Robbie Lee「Perspective Made Easy: A Step-by-Step Guide」

Robbie Lee「Perspective Made Easy: A Step-by-Step Guide」

This is a suitable book to pick up as the first one for learning the basics of perspective in general.

I found it to be simpler and more detailed than ‘Perspective! Learn Perspective Through Manga.’ Therefore, I especially recommend this book to beginners as their first read.

Scott Robertson「How to Draw: drawing and sketching objects and environments from your imagination」

Scott Robertson「How to Draw: drawing and sketching objects and environments from your imagination」

A book specialized in drawing, particularly focused on line art. Though somewhat complex, it provides a broad and in-depth explanation.

About the Japanese version of this article

This article is a translation of an article written in [https://souzoulog.com/2024/10/17/basic-of-perspective-3/]. For detailed references, please refer to this link.